跳转至

对称密码

一、基础知识

（一）异或运算(XOR，符号：\oplus)

运算规则：同为0，异为1
0 \oplus 0 = 0 1 \oplus 1=0
0 \oplus 1=1 1 \oplus 0=1

（二）常见三种运算符

  1. ^ ，异或计算
  2. | ，有1则1，全0才0
  3. & ，有0则0，全1才1

（三）奇偶校验

奇偶校验是一种校验代码传输正确性的方法。根据被传输的一组二进制代码的数位中“1”的个数是奇数或偶数来进行校验。

采用奇数的称为奇校验，反之，称为偶校验。采用何种校验是事先规定好的。通常专门设置一个奇偶校验位，用它使这组代码中“1”的个数为奇数或偶数。

用奇校验，则当接收端收到这组代码时，校验“1”的个数是否为奇数，从而确定传输代码的正确性。

（四）有限域上的乘法1

域

简单来说，域是可以执行加减乘和逆操作的集合。

伽罗瓦域（有限域）

有限域是由有限个元素组成的集合，在这个集合内可以执行加减乘和逆操作

定理： $ 只有当m是一个素数幂时，即m=p^n(其中n为正整数，p为素数)，阶为m的域才存在。P称为这个有限域的特征 $

tips：域所包含的元素个数称为域的阶或基

素数域

阶为素数的域，即n=1，域GF(p)的元素可以用整数0，1，……，p-1表示。域的两种操作是模整数加法和整数乘法模p

扩展域： 如果有限域的阶不是素数，则在这个有限域内加法和乘法操作就不能模p，$ m>1 $ ​​的域称为扩展域。扩展域的元素可以用多项式表示，且扩展域内的计算也可以通过某种多项式运算得到。

扩展域GF(2^m)

GF(2^m)： 在AES中包含256个元素的有限域可以用GF(2^8)。该域的每一个元素都可以用一个字节表示。

每个元素 $ A\in GF(2^8) $ 都可以表示为：$ A(x)=a_7x^7+……+a_1x+a_0, a^i\in GF(2)={0,1} $​

简单举例：$ 1=1,2=x,3=1+x,4=x2,5=1+x2,6=x+x^2,…… $

可以把1=1，$ x=10 ， x^2=100 ， x^3=1000 ，A\in GF(2^8)$的多项式某种程度上可以看作是十进制与二进制的转换

加法计算(即模2加法)：

模2加法，二进制加法，只留模2的余数，抛弃进位，即XOR

减法计算(即模2减法)：

模2减法，二进制减法，大数减小数，不借位，即XOR

乘法计算(即模2乘法)：

模2乘法是指在乘法竖式运算中需要做加法的地方都使用异或运算

下图红框中 1⊕0⊕1=0，没有进位：

5\times 7=(1+x^2)\times (1+x+x^2) \\ =1+x+x^2+x^2+x^3+x^4(mod 2) \\ =1+x+x^3+x^4=27

除法运算(即模2除法)：

模2除法是指在除法竖式运算中需要做减法的地方都使用异或运算。

下图红框中，0\oplus 1=1，没有借位：

二、分组密码（块密码）2

(一)定义

将明文消息分割成固定长度的数据块，并使用相同的密钥和算法对每个数据块进行加密

例：加密FOUR_AND_FOUR利用分组密码可以先加密FOUR，再加密 _AND_ ，最后加密FOUR，即一次加密明文中一个字符块

（二）分组模式

分为ECB（电子密码本）、CBC（密码块链接）、CFB（密码反馈），OFB（输出反馈），前两种模式使用分组密码，后两种模式将分组密码当作流密码使用，另外常见还有CTR（计数器），是OFB的变种

  1. ECB

一般给定密钥后，相同的明文块会有相同的密文块，如果明文块反复出现，对应的密文块也会多次出现，会为破解密文提供线索

加密：

img

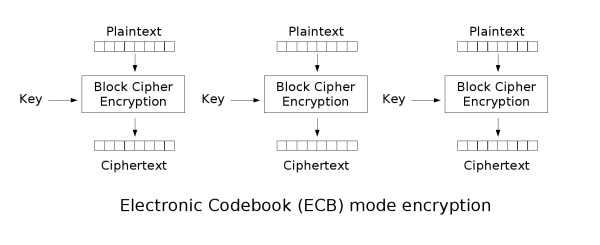
电子密码本仅适合加密短消息，明文重复少，破解几率低

解密：

img

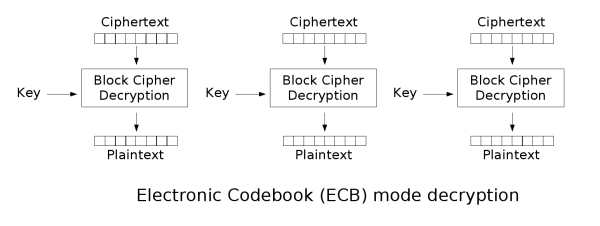
  1. CBC

    在块密码中增加反馈机制链接，即用每个块来修饰下一个块的加密

    加密：

    img

    (1) 如图所示，第1步有两个输入：第1个明文块和一个随机文本块。随机文本块是初始化向量（IV），没有特殊含义，只是为了使每个消息独特。将第1个明文块和IV异或再用密钥加密，生成密文块1

    (2) 将密文块1跟明文块2异或后再用密钥加密得出密文块2，依次类推

    注：IV仅在第1个明文块中使用，但用相同的密钥加密

    解密：

    img

  2. CFB

    数据加密单元更小（8位，即输入1个字符的大小）

    工作原理：

    (1) 和CBC一样使用64位IV，IV保存在移位寄存器里，用密钥加密IV得出密文

    (2) 将加密的IV最左边（即最高有效）的 j 位与明文的前 j 位进行异或，产生密文的第1部分，将密文C反馈给IV移位寄存器

    (3) IV移位寄存器左移 j 位，即IV所在的位移寄存器内容左移 j 位，因此IV移位寄存器最右j位为不可探测数据，用密文C填充最右 j 位

    (4) 重复以上步骤

完整加密过程：

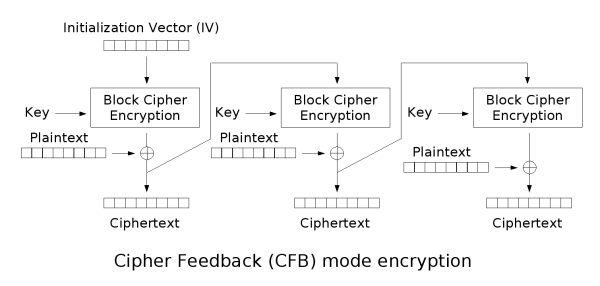
解密过程与加密过程非常相似，不过多赘述

  1. OFB

    OFB与CFB非常相似，唯一的区别是，CFB将密文反馈到加密过程下一阶段，OFB将IV加密过程的输出反馈到加密过程下一阶段

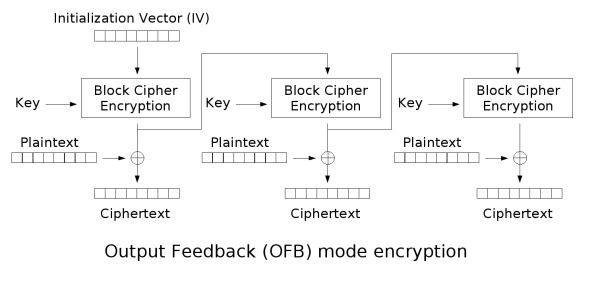
1
2
3
4
5
可以和CFB加密过程对比着来看

OFB的优势在于，个别位的错误只会影响个别位，不会破坏整个消息；缺点在于攻击者可以同时篡改密文和信息的校验和，而我们无法检测这种篡改

注：校验和就是通过对数据进行特定算法处理，生成一个简短的固定长度的校验码，附加在数据尾部。这个校验码的生成基于数据的每一位进行异或运算。如果数据中某一位发生变化，那么在校验码中这一位也会发生变化，从而检测到错误

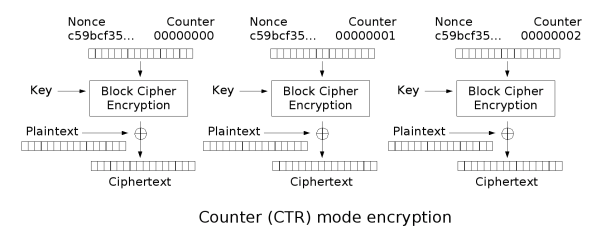
  1. CTR

    CTR是OFB的变种，用序列号（即计数器）作为输入，在加密每个块后，再使用下一个计数器值填充寄存器。通常使用一个常数作为计数器初始值，并且每次迭代后递增。计数器块的大小等于明文块的大小。CTR模式可以多个文本块并行处理。

（三）DES（数据加密标准）

加解密

DES使用56位的密钥和64位的明文块进行加密，初始密钥实际上也是64位，但在开始之前，丢弃了密钥的每个第8位，得到56位密钥。丢弃之前可进行奇偶校验，以确保密钥不包含任何错误。

（1）初始置换

初始置换只发生一次，且只发生在第一轮之前，例如，初始置换指定要将原始明文块的第1位替换成原始明文块的第58位，第2位替换成第50位等。

完成初始置换后，生成的64位置换明文块被分为两半，各32位，左半块是左明文(L0)，右半块是右明文(R0)，对这两块执行16轮操作

图 7

(2)获取子密钥

在进入第一轮之前，还需要对密钥进行处理生成子密钥，每一轮将使用不同的子密钥参与运算。DES加密算法的密钥长度为56位，一般表示为64位(每个第8位用于奇偶校验)，将用户提供的64位初始密钥经过一系列的处理得到K1,K2,…,K16，分别作为1~16轮运算的16个子密钥。

  1. 将64位密钥去掉8个校验位，用密钥置换PC-1置换剩下的56位密钥。

PC-1置换表如下

图 3

  1. 将56位分成前28位C0和后28位D0。

  2. 根据轮数，这两部分分别循环左移1位或2位

图 4

  1. 移动后，将两部分合并成56位后通过压缩置换PC-2后得到48位子密钥。

PC-2置换表如下

图 5

（3）Feistel网络

DES的基本结构，加密的各个步骤称为轮，DES是一种16轮循环的Feistel网络，下图为Feistel网络中的一轮

Feistel网络中的一轮

密码函数F的作用是将输入的32比特数据和48比特子密钥进行加密输出32比特

扩展置换E：将数据的右半部分Ri从32位扩展为48位。位选择函数(也称E盒)。

异或：扩展后的48位输出E(Ri)与压缩后的48位密钥Ki作异或运算；

S盒替换：将异或得到的48位结果分成八个6位的块，每一块通过对应的一个S盒产生一个4位的输出。（8个不同s盒压缩处理）

P盒置换：将S盒得到的输出再和P盒进行置换操作。

  • 一轮下来”右侧“并没有被加密，需要不同的子密钥重复若干次，并在每两轮处理之间将左右数据对调
  • 3轮加密需要两次左右对调，对调只在两轮之间进行，最后一轮结束之后不需要对调
  • 解密只需要照相反顺序使用子密钥就可以
(4)逆置换

也叫最终置换，DES加密过程最后的逆置换IP−1，是初始置换的逆过程。经过16次迭代运算后，进行逆置换，即得到密文输出。逆置换正好是初始置的逆运算。例如，第1位经过初始置换后，处于第40位，而通过逆置换，又将第40位换回到第1位。

（四）AES（高级加密标准）

AES使用的是Rijndael算法，SPN结构。Rijndael算法与DES的主要区别在于Rijndael的所有操作都是涉及整个字节的，而非字节的单个位

1. 加解密

轮密钥加： 明文矩阵P，子密钥矩阵K，轮密钥加的结果就是两个矩阵对应元素异或

字节替换： 引入一个S盒，置换逻辑是通过s表完成一个字节到另一个字节的映射，比如矩阵第一个元素是19，找s盒里第1行第9列的数替换

行置换： 目的是为了达到雪崩效应，一点微小变化也会导致输出有大改变，逻辑是第一行不变，第二行左移1，第三行左移2，第四行左移3

列混淆： 将给定矩阵和P在GF(2^8)做乘法。

2. python实践

(1)创造加密对象
  • 使用Crypto.Cipher.<algorithm>.new(key,mode)创造对称加解密对象。key表示对称算法密钥；mode表示分组加密模式，常见模式有ECB、CBC等；<algorithm>表示加密算法，例如AES
  • 语句：Crypto.cipher.AES.new(a,b,c) 或是cipher=AES.new(a,b,c)（from...import ASE才能用）
  • a是密钥，格式一般是key=b'018w'，b''的作用是把密钥转换成bytes类型
  • b是模式的确定，例如AES.MODE_CBC，模式为CBC模式
  • c是初始偏移量iv
（2）填充(padding)

对称加密算法在使用过程中，每次是对固定大小的分组数据进行加密。但真实的待加密数据几乎都不是分组长度的倍数，需要对数据进行填充，将加密输入的数据长度补齐至分组长度的倍数。

在python用的是pycryptodome库中Crypto.Util.Padding这个模块里的pad和unpad

  • Crypto.Util.Padding.pad(FOUR_AND_FOUR,block_size,style='pkcs7') 负责进行数据填充，其中FOUR_AND_FOUR 表示待填充的数据；block_size 表示用于填充的分组长度；style 表示填充算法，一般默认为pkcs7，其他填充算法参考 https://en.wikipedia.org/wiki/Padding_(cryptography)； 以上皆为输入参数，输出是填充后的数据，数据类型为byte
  • Crypto.Util.Padding.unpad(FOUR_AND_FOUR,block_size,style='pkcs7') 负责进行填充后的数据解析，得到原始数据，输出为移除填充后的原始数据，数据类型仍为byte
(3)加密与解密
  • 创建加密对象cipher=AES.new(key,AES.MODE_CBC)
  • 用cipher.encrypt(data)加密
  • 用cipher.decrypt(date)解密
  • 加密解密输出的数据类型都为byte 示例 
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
    from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes
from Crypto.Util.Padding import pad,unpad

#加密
key = get_random_bytes(16)
iv = get_random_bytes(AES.block_size)#创建AES.block_size个byte的随机数，AES.block_size为16
cipher = AES.new(key,AES.MODE_CBC,iv)
data = b'Hunsec={Hello_AES_CBC}'
ciphertext = cipher.encrypt(pad(data,AES.block_size))
print("key=",key)
# key=
b'\x9d\x9c>\x15t\xcf\xc4\xdc9\xbc|j\x95\xbe\xc9\x02'
print("iv=",iv)
# iv= b'\xf6HS\xfeUpzRo\xa3\xeaiX\xd9\x9d\xa1'
print("ciphertext=",ciphertext)
# ciphertext= b'<b\xcaj\xec\xc4EA|\x7f\xc1\xe8\xa5\x1e\xeb\t\x00`\x80\xec\\\x967\x0bB\xa3\xae\x15\x96\xf9FG'

流密码

（一）定义

流密码是加密和解密双方使用相同伪随机加密数据流作为密钥，明文数据每次与密钥数据流顺次对应加密，得到密文数据流。实践中数据通常是一个位（bit）并用异或（XOR）操作加密 可以理解成明⽂ \oplus ‘密钥’，但是密钥是由⼀个伪随机数⽣成器⽣成的

（二）伪随机数生成器（PRG/PRNG）

伪随机序列：如果一个序列能够和等长的随机序列不可区分的话，那么它就是伪随机序列，即可以以假乱真的序列

判断序列是否随机，不能以貌取人，真随机丢硬币也有丢出来全1的概率，有规律 ≠ 不随机

伪随机密钥流：

1. 线性同余生成器（LCG）3

LCG的原理是通过一个递归公式生成下一个随机数，包含一个乘法因子、一个加法常数和一个模数。

X_{n+1}= AX_n+B(mod m)，\\ 其中乘法因子0<A<m，加法常数0 \le B<m，模数m>0

$A=13,B=17,m=22,X_n=8 $ $ X_{n+1}=(13\times 8+17)mod 22\ =121 mod 22=11$

python实践

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
import time
seed = int(time.time())
a=13
b=17
m=22
def generate_random(seed):
    while True:
        seed = (a * seed + b ) % m
        yield seed

random_generator=generate_random(seed)

for i in range(20):
    random_number = next(random_generator)
    print(random_number)

2. 线性反馈移位寄存器（LFSR）4

img

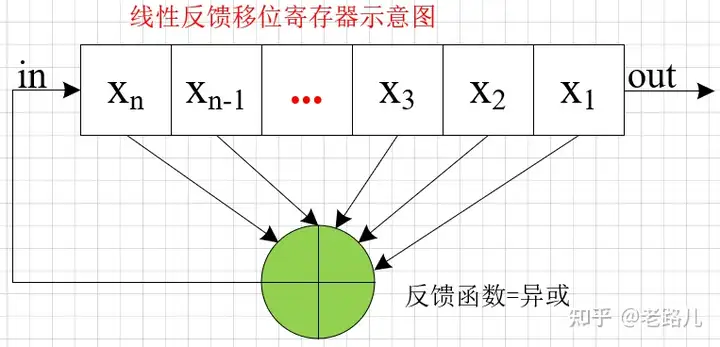
python实现

1
2
3
4
5
state = 0b1101
for i in range(16):
    print("{:04b}".format(state))
    newbit = (state^(state>>1))&1
    state = (state>>1)|(newbit<<3)

讲义写的一般，请大家多担待，一些公式显示问题，复制到自己的markdown文件就能看了

作业在http://ctf.miaoaixuan.cn/ ,希望能帮大家加深对AES、DES、LCG的理解

  1. 参考Alice-Bob的密码学数学基础,《深入浅出密码学——常用加密技术原理与应用》，模2运算 ↩

  2. 定义，加解密，前4组分组模式参考《密码学与网络安全(第4版)》，校内图书馆可借，推荐借阅第3版，第4版有部分印刷问题；CTR和DES参考《图解密码技术(第3版)》；AES及代码实践参考《密码技术应用与实践》西安电子科技大学出版社，校内图书馆可借；AES及DES部分参考NSSCTF工坊对称密码部分；图片部分来源CTFWIKI ↩

  3. 参考原理lcg（线性同余生成器）原理加各种题目（第一部分），代码来自线性同余生成器python ↩

  4. 该部分参考【计算机】使用LFSR线性反馈移位寄存器的随机数！ ↩

评论