ctf——Crypto¶
CTF(Capture The Flag)是信息安全领域中一种极具挑战性和趣味性的竞赛形式,参赛者通过破解各种加密、解密、编程和逆向工程等任务来获得“旗帜”(Flag)。在CTF竞赛中,密码学方向的任务主要涉及各种加密算法、解密技巧和密码破解的应用。具体来说,CTF密码学方向的任务通常包括经典密码破解(如凯撒密码、维吉尼亚密码等)、现代加密算法的攻击、密钥恢复、哈希碰撞以及密码协议的漏洞分析等。
需要运用对密码学知识的理解和实际操作技能,解决与加密算法、密文分析、数据泄露、漏洞利用等相关的问题。这考验了选手对密码学理论的掌握,还要求具备一定的编程能力、逆向思维以及创新性的解决问题的能力。CTF密码学方向的任务既可以是理论性的,如对传统密码学算法的分析,也可以是实践性的,如模拟现代加密算法的攻击。
Crypto方向题目类型:¶
1. 经典加密算法破解¶
- 对称加密(如AES、DES):这些题目通常会给出加密文本和一些已知信息(比如密钥、明文等),考察选手如何通过分析和算法攻击破解加密数据。
- 非对称加密(如RSA、ECC):RSA是CTF比赛中最常见的加密方式之一,题目可能包括公钥加密、私钥泄漏、密钥恢复、数字签名等,一般需要利用数学知识(如素因数分解、扩展欧几里得算法)破解这些加密。
- 哈希函数(如MD5、SHA):这些题目一般会给出某个哈希值,要求选手找出原始数据,或是利用碰撞攻击、字典攻击等方法破解哈希值。
2. 编码和加密算法的组合¶
- 很多Crypto题目涉及到某种加密算法与编码方式(如Base64、Hex、URL编码等)结合,需要首先解码,再进行加密破解或逆向解密。
3. 流密码与分组密码¶
- 流密码(如RC4):流密码生成的加密文本可能与某种特定的结构有关,需要通过分析密文流来恢复密钥。
- 分组密码(如DES、AES):这类题目中,密文可能采用了某种模式(如ECB、CBC),破解时需要注意模式的特性,并利用它们的弱点进行攻击。
4. 密码学漏洞利用¶
- 这些题目通常会涉及到加密算法的漏洞或设计缺陷,选手需要找到漏洞并利用它进行破解。常见的漏洞包括时间攻击、侧信道攻击、重放攻击、密钥恢复等。
- 例如,某些加密算法可能使用不安全的随机数生成器,或者密钥长度不够,攻击者可以利用这些弱点进行攻击。
5. 数学问题¶
- 密码学问题往往需要一定的数学基础,特别是数论、代数、概率论等。常见的数学题目包括素数分解、离散对数问题、欧几里得算法等。
- 例如,RSA加密的安全性基于大数分解的困难性,所以如果你能利用某些优化算法对大数分解进行攻击,就能破解RSA。
6.古典密码¶
古典密码(Classical Cryptography)是指在现代计算机技术普及之前使用的加密技术,通常是通过简单的数学或逻辑方法来对信息进行加密和解密。常见的有凯撒密码、单表替换密码、栅栏密码、维吉尼亚密码、摩尔斯密码等等。
数论基础¶
1.整除¶
定义¶
设 







例子¶
整除的性质¶
- 自反性:对于任何整数
,都有
。
- 传递性:如果
且
,那么
。
- 线性组合:如果
且
,那么对于任何整数
和
,都有
。
- 倍数性质:如果
,那么对于任何整数
,都有
。
- 因数性质:如果
且
,那么
。
- 唯一性:如果
且
,那么
。
2.同余¶
定义¶
设 










例子¶
同余的性质¶
- 自反性:对于任何整数
和正整数
,都有
。
- 对称性:如果
,那么
。
- 传递性:如果
且
,那么
。
- 线性组合:如果
且
,那么对于任何整数
和
,都有
- 乘法性质:如果
,那么对于任何整数
,都有
。
- 除法性质:如果
且
是
和
的公因数,
3.逆元¶
定义¶
在数论中,逆元通常指的是模







此外,逆元的范围属于1 ~(m-1)
例子¶
- 求 3模 7 的逆元:
- 我们需要找到一个整数
,使得
。
。
- 因此,3 模 7的逆元是 5
- 我们需要找到一个整数
- 求 2 模 9 的逆元:
- 我们需要找到一个整数
,使得
。
- 因此,2 模 9的逆元是 5。
- 我们需要找到一个整数
逆元的性质¶
- 唯一性:如果 a 模 m的逆元存在,那么它是唯一的。
- 存在性:a模 m 的逆元存在当且仅当 a和 m互质,即
。
- 逆元的逆元:如果 b是 a模 m的逆元,那么 a是 b模 m的逆元。
4.欧拉函数¶
定义¶
在数论中,欧拉函数 


性质¶
- 积性函数:如果
和
互质,即
那么
:显然,1 与任何数互质。
- 质数的欧拉函数:对于质数
- 质数幂的欧拉函数:对于质数的幂
- 一般计算公式:如果
,其中
是质数,
为正整数,那么
例子¶
- 计算 ϕ(10):
- 小于或等于 10 的正整数中与 10 互质的数有:1, 3, 7, 9。
- ϕ(10)=4。
- 计算 ϕ(12)
- 小于或等于 12 的正整数中与 12 互质的数有:1, 5, 7, 11。
- ϕ(12)=4
5.欧拉定理¶
定义¶
欧拉定理(Euler's Theorem)是数论中的一个重要定理,它描述了模运算中的一些性质。具体来说,对于任意整数 






例子¶
- 计算
的最后两位数:
- 首先,我们需要计算
。因为
,所以:
- 由于
,根据欧拉定理,我们有:
- 因此:
- 最后两位数是 27。
- 首先,我们需要计算
6.费马小定理¶
费马小定理(Fermat's Little Theorem)是数论中的一个基本定理。具体来说,如果



例子¶
计算 :
费马小定理的应用¶
费马小定理在数论、密码学、计算机科学等领域有广泛的应用。例如,在RSA 加密算法中,费马小定理被用来简化模幂运算。此外,费马小定理还可以用于素性测试,即判断一个数是否为质数。
7.群¶
群是一个集合

- 封闭性:对于所有
,运算
的结果也在
中。
- 结合律:对于所有
,有
- 单位元:存在一个元素
,使得对于所有
,有
- 逆元:对于每个
,存在一个元素
,使得
例子:
- 整数集合
在加法运算下构成一个群,单位元是 0,每个元素
逆元是
- 非零有理数集合
在乘法运算下构成一个群,单位元是 1,每个元素
的逆元是
RSA¶
密钥生成¶
RSA密钥生成包括以下步骤: ①选择两个大质数p和q ②计算n=pq ③欧拉公式φ(n)=(p-1)(q-1)
④选择一个整数e,使得1<e<φ(n),且e和φ(n)互质
⑤计算e关于φ(n)的模逆元d,即ed≡1(mod φ(n)) 此时就能得到公钥pk=(e, n),私钥sk=(d, n)
RSA加密和解密¶
给定明文M,加密过程如下:
- 计算C≡M**e (mod n),得到的C就是密文。
给定密文C,解密过程如下:
- 计算M≡C**d (mod n),得到的M就是解密后的明文。
对称密码¶
一、基础知识¶
(一)异或¶
运算规则:同为0,异为1
| 0⊕0=0 | 1⊕1=0 |
|---|---|
| 0⊕1=1 | 1⊕0=1 |
(二)常见三种运算符¶
- ^ ,异或计算
- | ,有1则1,全0才0 (析取)
- & ,有0则0,全1才1(合取)
(三)奇偶校验¶
奇偶校验是一种校验代码传输正确性的方法。根据被传输的一组二进制代码的数位中“1”的个数是奇数或偶数来进行校验。
采用奇数的称为奇校验,反之,称为偶校验。采用何种校验是事先规定好的。通常专门设置一个奇偶校验位,用它使这组代码中“1”的个数为奇数或偶数。
用奇校验,则当接收端收到这组代码时,校验“1”的个数是否为奇数,从而确定传输代码的正确性。
(四)有限域¶
有限域是包括有限个元素、能进行加减乘除运算的集合
- 单位元:任何元素与单位元做运算,得到的都是该元素,单位元是唯一的。
- 逆元:A与B做运算,得到的结果是单位元,则A和B互为该运算下的逆元
- 封闭性:运算元素和结果都在域中有对应元素
- 结合律
- 交换律
- 分配律
- 无零因子
用处:将四则运算精简为二则运算加和乘
有限域GF(p)¶
p一定为素数,运算是模p的运算,域中有p个元素,p为素数保证每个元素都有加法和乘法逆元
例:GF(p),其中 p = 7
- 加:(a\oplus b)(mod\ 7)=(a+b)(mod\ 7)
- 减:(a\ominus b)(mod\ 7)=(a+(-b))(mod\ 7),-b为 b 的加法逆元
- 乘:(a\otimes b)(mod\ 7)=(a\times b)(mod\ 7)
-
除:(a\oslash b)(mod\ 7)=(a/ b)(mod\ 7)=(a\times(b^{-1}))(mod\ 7),b^{-1}是 b 的乘法逆元
在这里,已知5\otimes 3=1,所以6\oslash5=6\otimes3=4,除法运算要求在有限域GF(7)内,满足封闭性
符合二进制的域GF(2^m)¶
GF(2):只有0和1元素,01相加减都需要模2,符合异或运算
扩展域: 如果有限域的阶不是素数,则在这个有限域内加法和乘法操作就不能模p,$ m>1 $ 的域称为扩展域。扩展域的元素可以用多项式表示,且扩展域内的计算也可以通过多项式运算得到。
扩展域GF(2^m): 在AES中包含256个元素的有限域可以用GF(2^8)。该域的每一个元素都可以用一个字节表示。
每个元素 $ A\in GF(2^8) $ 都可以表示为:$ A(x)=b_7x^7+……+b_1x+b_0, b_i\in GF(2)={0,1} $
简单举例:$ 1=1,2=x,3=1+x,4=x2,5=1+x2,6=x+x^2,…… $
运算¶
加法: 异或
例:57+66=01010111+01100110=00110001=31,这里的57、66和31均为16进制
乘法: 先乘再加,最后模,这里的模多项式采用m(x)=x^8+x^4+x^3+x+1 $$ 57\times 66=01010111\times 01100110\ =(x6+x4+x^2+x+1)\times (x6+x5+x^2+x)\ =x{12}+x+x8+x7+x6+x+x9+x7+x6+x5\ +x8+x6+x4+x3+x2+x7+x5+x3+x^2+x\ =x{12}+x+x{10}+x9+x7+x6+x4+x(mod x8+x4+x3+x+1)\ =x7+x5+x4+x3+x+1 $$
二、分组密码¶
定义:将明文消息分割成固定长度的数据块,并使用相同的密钥和算法对每个数据块进行加密
例:加密FOUR_AND_FOUR利用分组密码可以先加密FOUR,再加密_AND_ ,最后加密FOUR,即一次加密明文中一个字符块
(一)分组模式¶
分为ECB(电子密码本)、CBC(密码块链接)、CFB(密码反馈),OFB(输出反馈),前两种模式使用分组密码,后两种模式将分组密码当作流密码使用,另外常见还有CTR(计数器),是OFB的变种
- ECB
一般给定密钥后,相同的明文块会有相同的密文块,如果明文块反复出现,对应的密文块也会多次出现,会为破解密文提供线索
加密:
电子密码本仅适合加密短消息,明文重复少,破解几率低
解密:
- CBC
在块密码中增加反馈机制链接,即用每个块来修饰下一个块的加密
加密:
(1) 如图所示,第1步有两个输入:第1个明文块和一个随机文本块。随机文本块是初始化向量(IV),没有特殊含义,只是为了使每个消息独特。将第1个明文块和IV异或再用密钥加密,生成密文块1
(2) 将密文块1跟明文块2异或后再用密钥加密得出密文块2,依次类推
注:IV仅在第1个明文块中使用,但用相同的密钥加密
解密:
关于填充,一般情况下明文长度是不符合分块要求的,需要对此进行填充。
常见填充方式如下:
- ISO 10126: 规定应在最后一个块的末尾用随机字节进行填充,填充边界应由最后一个字节指定。
这种填充方式中,填充字符串的最后一个字节为填充字节的长度,其他为随机字节
例如:现在有3bytes,块大小为8bytes,需要填充5bytes,则最后一个为 05,其他全部为 00
原数据:66 6F 72
填充后的数据:66 6F 72 81 A3 00 23 05
- PKCS7: 假设需要填充n (n>0) 个字节才对齐,填充n个字节,每个字节都是n ;如果数据本身就已经对齐了,则填充一块长度为块大小的数据,每个字节都是块大小;PKCS7填充字节的范围在 1-255 之间 ,填充方式为上面的 填充数据为填充字节的长度,填充如下:
1 2 3 4 5 6 | |
当且仅当N小于256时才有用。
原数据:66 6F 72
填充后的数据:66 6F 72 05 05 05 05 05
-
PKCS5: 将数据填充到8的倍数,填充数据计算公式是,假如原数据长度为len,利用该方法填充后的长度是 len + (8 - (len % 8)), 填充的数据长度为 8 - (len % 8),块大小固定为8字节,和PKCS7的区别在于,5的填充块大小为8bytes,而7的填充块大小可以在1-255bytes之间。
-
ISO/IEC 7816-4: 第一个字节是值为 '80' (十六进制) 的强制字节,如果需要,后跟 0 到 N − 1 个设置为 '00' 的字节,直到到达块的末尾
例如:66 6F 72 80 00 00 00 00
- Zero padding: 所有需要填充的字节都用零填充。比如66 6F 72 00 00 00 00 00。它通常应用于二进制编码的字符串(以null 结尾的字符串),因为null字符通常可以作为空格被剥离。
(二)DES¶
DES使用56位的密钥和64位的明文块进行加密,初始密钥实际上也是64位,但在开始之前,丢弃了密钥的每个第8位,得到56位密钥。丢弃之前可进行奇偶校验,以确保密钥不包含任何错误。
(1)初始置换¶
初始置换只发生一次,且只发生在第一轮之前,例如,初始置换指定要将原始明文块的第1位替换成原始明文块的第58位,第2位替换成第50位等。
完成初始置换后,生成的64位置换明文块被分为两半,各32位,左半块是左明文(L0),右半块是右明文(R0),对这两块执行16轮操作

(2)获取子密钥¶
在进入第一轮之前,还需要对密钥进行处理生成子密钥,每一轮将使用不同的子密钥参与运算。DES加密算法的密钥长度为56位,一般表示为64位(每个第8位用于奇偶校验),将用户提供的64位初始密钥经过一系列的处理得到K1,K2,…,K16,分别作为1~16轮运算的16个子密钥。
- 将64位密钥去掉8个校验位,用密钥置换
PC-1置换剩下的56位密钥。
PC-1置换表如下

-
将56位分成前28位C0和后28位D0。
-
根据轮数,这两部分分别循环左移1位或2位

- 移动后,将两部分合并成56位后通过压缩置换
PC-2后得到48位子密钥。
PC-2置换表如下

(3)轮函数f¶
轮函数F的作用是将输入的32比特数据和48比特子密钥进行加密输出32比特
扩展置换E:将数据的右半部分Ri从32位扩展为48位。位选择函数(也称E盒)。
异或:扩展后的48位输出E(Ri)与压缩后的48位密钥Ki作异或运算;
S盒替换:将异或得到的48位结果分成八个6位的块,每一块通过对应的一个S盒产生一个4位的输出。(8个不同s盒压缩处理)
| \ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 |
| 1 | 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 |
| 2 | 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 |
| 3 | 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 |
例如输入101010到S1中。S1会将这六位的第一位和第六位拿出来10作为S1的行,中间四位0101拿出来作为S1的列。我们转换成十进制,此时映射到这个S盒的位置就是(2,5)对应S盒的第3行第6列(索引都从0开始数)。

P盒置换:将S盒得到的输出再和P盒进行置换操作。

(4)逆置换¶
也叫最终置换,DES加密过程最后的逆置换IP−1,是初始置换的逆过程。经过16次迭代运算后,进行逆置换,即得到密文输出。逆置换正好是初始置的逆运算。例如,第1位经过初始置换后,处于第40位,而通过逆置换,又将第40位换回到第1位。置换表如下:

(三)AES¶
1. 加密¶

**秘钥扩展 ** 示例秘钥key = “abcdefghijklmnop”={0x61, 0x62,…,0x6F,0x70}。 AES128中原始秘钥key为16字节,运算中需要11个矩阵大小的秘钥,每一列所包含的32位记为一个uint32_t W,所以秘钥扩展一共需要生产44个列W,即uint32_t W[44]。
W[0-3]为直接复制的原始秘钥。
W[0] = 0x61626364. W[1] = 0x65666768. W[2] = 0x696A6B6C. W[3] = 0x6D6E6F70. W[4-43]为扩展的秘钥。

Mix(x)=SubWord(RotWord(x))
RotWord()为循环左移一位
SubWord()为字节替换
rcon为轮常量异或,常量数组为:

下面举个例子: 设初始的128位密钥为: 3C A1 0B 21 57 F0 19 16 90 2E 13 80 AC C1 07 BD 那么4个初始值为: W[0] = 3C A1 0B 21 W[1] = 57 F0 19 16 W[2] = 90 2E 13 80 W[3] = AC C1 07 BD 下面求扩展的第1轮的子密钥(W[4],W[5],W[6],W[7])。 由于4是4的倍数,所以: W[4] = W[0] ⨁ T(W[3]) T(W[3])的计算步骤如下:
循环地将W[3]的元素移位:AC C1 07 BD变成C1 07 BD AC; 将 C1 07 BD AC 作为S盒的输入,输出为78 C5 7A 91; 将78 C5 7A 91与第一轮轮常量Rcon[1]进行异或运算,将得到79 C5 7A 91,因此,T(W[3])=79 C5 7A 91,故 W[4] = 3C A1 0B 21 ⨁ 79 C5 7A 91 = 45 64 71 B0 其余的3个子密钥段的计算如下: W[5] = W[1] ⨁ W[4] = 57 F0 19 16 ⨁ 45 64 71 B0 = 12 94 68 A6 W[6] = W[2] ⨁ W[5] =90 2E 13 80 ⨁ 12 94 68 A6 = 82 BA 7B 26 W[7] = W[3] ⨁ W[6] = AC C1 07 BD ⨁ 82 BA 7B 26 = 2E 7B 7C 9B 所以,第一轮的密钥为 45 64 71 B0 12 94 68 A6 82 BA 7B 26 2E 7B 7C 9B。
轮密钥加: 明文矩阵P,子密钥矩阵K,轮密钥加的结果就是两个矩阵对应元素异或
字节替换: 将字节看作GF(2^8)上的元素,根据s盒做映射,然后对字节做如下的(GF(2)上可逆的)仿射变换
行移位: 第一行不变,第二行左移1,第三行左移2,第四行左移3
列混淆: 列混合通过矩阵相乘来实现,经过移位后的矩阵左乘一个固定的矩阵,得到混淆后的矩阵,如下公式所示

上述矩阵相乘可以化简为如下表达式:

其中矩阵的乘法和加法并不是通常意义上的乘法和加法,而是定义在伽罗华域上的二元运算,且使用的不可约多项式为P ( x ) = x 8 + x 4 + x 3 + x + 1 。其加法为模二加法,相当于异或运算,其乘法可以使用GMul表示,则上式运算可以表示为

解密时逆列混合操作和列混合一样,只是左乘的矩阵使用如下矩阵。可以验证此矩阵B是列混合使用矩阵A的逆矩阵,两者乘积为单位矩阵,即AB=BA=E

2. 解密¶
- 交换逆向行移位和逆向字节代替并不影响结果
- 交换轮密钥加和逆向列混淆并不影响结果,关键在于首先可以把异或看成域上的多项式加法,然后多项式中乘法对加法具有分配律
加解密全图
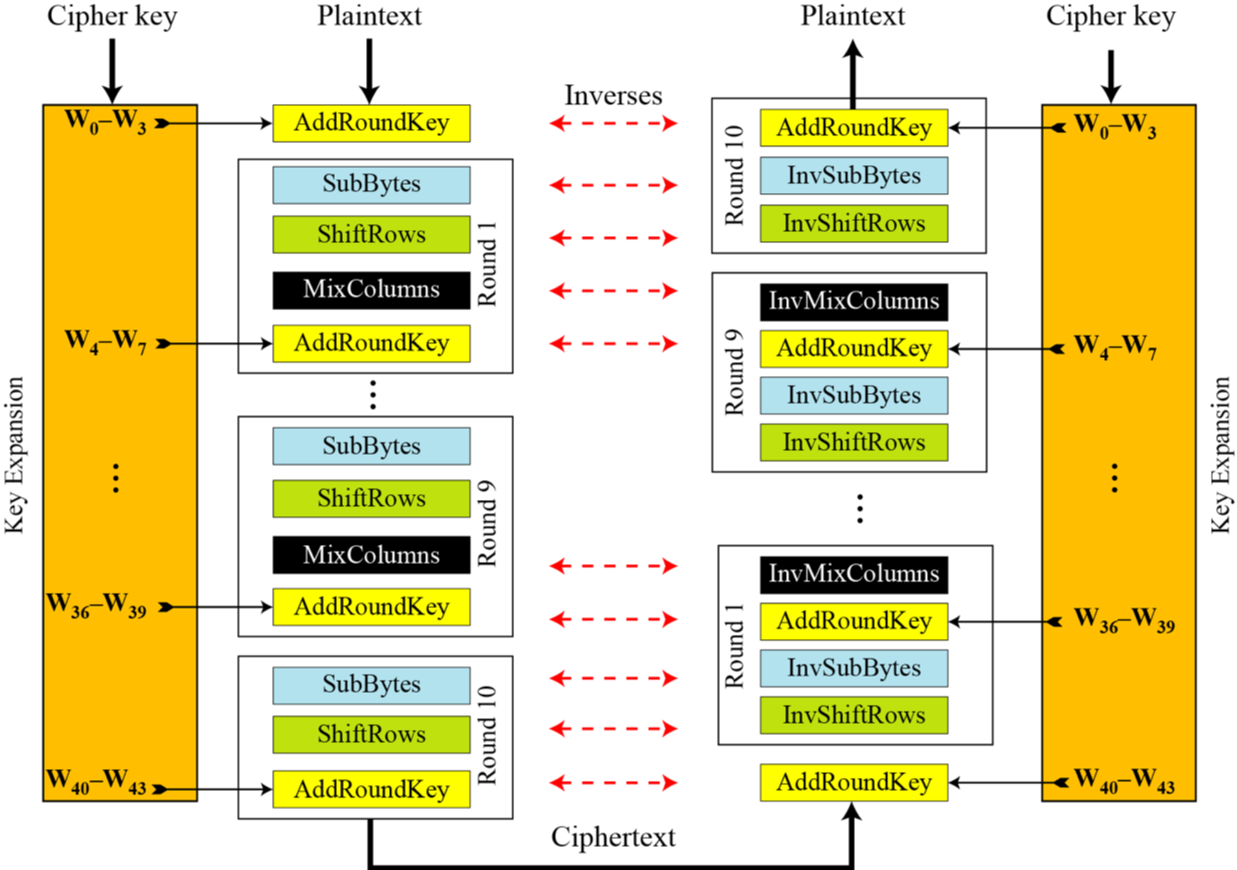
三、流密码¶
定义:流密码是加密和解密双方使用相同伪随机加密数据流作为密钥,明文数据每次与密钥数据流顺次对应加密,得到密文数据流。实践中数据通常是一个位(bit)并用异或(XOR)操作加密 可以理解成明⽂ ⊕ 密钥,但是密钥是由⼀个伪随机数⽣成器⽣成的
PRG/PRNG伪随机数生成器¶
伪随机序列:如果一个序列能够和等长的随机序列不可区分的话,那么它就是伪随机序列,即可以以假乱真的序列
LCG线性同余生成器¶
LCG的原理是通过一个递归公式生成下一个随机数,包含一个乘法因子、一个加法常数和一个模数。 $$ X_{n+1}=AX_n+B(mod m)\ 其中乘法因子0<A<m,加法常数0≤B
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | |



















